Fractals

Fractals are a branch of mathematically defined algorithms that are most commonly used to generate complex computer images.

The Ogless fractal explorer lets you explore these amazing fractal landscapes. You can download and install the screen saver for free from our download page.

The computation could not be any simpler, it involves the repeated squaring of a complex number (a number with real and imaginary parts).

a = x + iy;
a2 = (x+iy) * (x+iy);
a2 = x2 + 2iy + i2y;
a2 = x2 - y2 + 2ixy;

The real part of the result (x² - y²) and the imaginary part (2ixy) are then passed to the next iteration as the new x and y. The standard fractal set is produced in graphical form by counting how many times this loop is executed before (x² + y²) exceeds a certain value. The count of loop iterations is then converted to a color value and plotted according to the value of the initial position (x,y) value.

Without knowing the details of what the function does it is clear that an initial point very close to the origin (x=0; y=0) will take a very large number of iterations to reach (may be never) the limit. While a point far from the origin will take very few iterations to reach this threshold value. It is the small region in between the two extremes that generates all the 'pretty' fractal patterns.

Fractal code in C++

double Fx, Fy, Initx, Inity, Sqx, Sqy;
int Loops;

Fx = Initx;
Fy = Inity;
for (Loops = 0; Loops < MAX_LOOP_ITERATIONS; Loops++)
{
  Sqy = Fy*Fy;
  Sqx = Fx*Fx;
  if (Sqx + Sqy > 2.0) break;
  Fy = 2.0*Fx*Fy + Inity;
  Fx = Sqx - Sqy + Initx;
}
// Plot the value of 'Loops' as a color for the initial position Initx, Inity
// ...


The World of Fractals

The most surprising feature of the Mandelbrot ➚ and Julia sets is that the intricate detail revealed is infinite in depth. If you zoom in on a small region then the smaller region is broadly similar to the larger one, and you can zoom in indefinitely - up to the limits of the capabilities of the processor. When you see a typical part of the fractal set you'll see spirals made up of spirals, each smaller spiral is a miniature version of the larger version.

This image is the familiar Mandelbrot 'top level' picture. You can begin to see the intricate spirals that occur throughout the set. To demonstrate the way that zooming in on a fractal works go and Explore an Ogless image. Although these fractals have infinite depth the explorer is limited by the size of double precision floating point arithmetic available.

The concept has been broadened to a general 'fractal' concept for anything that is similar on one scale than on another scale. There are many different fractal algorithms that have been discovered. It is a powerful concept that can be applied to many fields of knowledge.

Fractals in the real world

The clearest example of a general fractal concept working in real-life comes from something amazingly simple. How do you measure the length of the coastline? It seems on face value a silly question, I just take a map and move around the coast totting up each mile measured. But then by doing this you are making an approximation, the coastline wiggles in and out and you should really take account of each cove and inlet. So the first figure is too low, but then where do you stop? When computing the length of coastline should you get the most detailed map and go around every cliff outline? But it does not stop there, as you can then consider whether each rock provides an extra level of detail that needs to be added. Moving from coves and beaches to rocks is one 'fractal' level as we then hit another consideration. Should each and every rock be considered? Some rocks are very angular and going into each pit and protrusion would greatly add to the total. Even smooth rocks are made up of very angular crystals under a microscope. The search goes on down to the molecular and atomic scale. The coastline can be considered infinite in length, it all depends what level of detail you stop looking any further at. The fractal levels identified are bay/cove/rock/crystal/molecule all with internal structure.

Mathematically this is an awkward situation to accommodate, the land area of an 'island' has a finite value but the island's coastline (perimeter) is arbitrary - effectively infinite. This is a big step away from Euclid ➚'s world of perfect lines and objects where the calculation of perimeter is simple to compute and a fixed relation to the area. For example a circle has area πr² and perimeter (circumference) 2πr for radius r. A fractal circle of the same area could have an arbitrary long perimeter, the Euclidean 2πr is the minimum possible perimeter - the edge in the rel world will be jagged to some degree. This is why Mandelbrot's work is so important in modeling real world objects - it takes account of the randomness that 'perfect' Euclidean objects do not possess. It has applications to model turbulent flow, dust, stars, rivers, Brownian motion ➚ and numerous other practical applications.

Another example of fractal scales is astronomical orbits. The moon goes around the Earth, the planets around the Sun, the Sun around the Galaxy and the Galaxies around the Galactic cluster. Also consider road networks, start at the motorway or inter-state highways and then main roads, small roads and lanes, they are all roads but differ in scale.

The interest in 'levels' of fractal has led to its application to human affairs. Can the rules and structures at the level of a state be applied to companies, cities and individuals? Re-using the same concepts at different levels can greatly simplify the situation. In software design it is also appealing to re-use the same set of procedures and functions on different objects at a different scale. Often finding a set of fractal levels not only simplifies design but simplifies the understanding of a system as there are fewer concepts to take in.

Unlimited zoom

On a computer a fractal is usually computed using floating point arithmetic as this keeps the same level of accuracy for very and very small numbers however it is still only an approximation and there comes a point where floating point 'rounding' and other errors creep in and affect the result. If you 'zoom' in a long way on a PC you will end up with a 'blocky' pixelated image just because of the limited size of representation of the number on it. If the floating point calculation uses a larger mantissa (more bits) then these effects will be delayed for longer. Intrinsically, as far we can tell the fractal set contains an infinite amount of detail, you never reach a point where there is no smaller structure.

Ogless's fractals

The standard fractal algorithm (Mandelbrot Set ➚) is quite appealing but lacks something. It is just a bit too repetitive and regular. There are lots of interesting spirals but they all look somewhat similar even with different colors. What Ogless has set out to do is to create new algorithms unique to Ogless that enliven the displayed fractal image. It does this by making slight changes to the basic fractal computation - adding extra parameters and modifying others. We have ended up with over a dozen of different variations of the fractal algorithm.

Here are the top level pictures of some of the algorithms that Ogless uses. In each case there is a controlling variable (called 'z') that substantially alters the pattern created, so there are an infinite number of these top level views, we have chosen an arbitrary one.

Original

The original, unchanged base algorithm - plain a' = a². All the frilly outer margins are somewhat similar when they are zoomed into.

First

This was the first successful attempt to create a different form of the fractal that had interesting areas when they are explored in detail.

Lace

The lace algorithm produces a very heavy distortion of the original form. It produces a lot of dots and swirls but in a linear and non-fractal form.

Superimpose 1

One way to perturb the basic fractal is to superimpose two slightly offset original fractals. This creates areas of discontinuity but the basic structure is the same.

Contorted

One of the first variants of the algorithm to be discovered. It is a mixture of ‘Julia ➚’ and ‘Mandelbrot’ areas spread over the area.

Sine wave

One way to produce distortions to the original fractal is to combine it with another totally different algorithm. In this case the standard sine wave was chosen. It creates some interesting areas of distortion.

Z Step

In this case an iteration builds up a linear distortion that feeds back into the algorithm. It creates some 'zip-like' areas that break up the original form.

Squash

The distortions created in this version tend to bend and squash the original geometry.

Break

This chance discovery opened up a new class of fractal algorithms. Most of the previous super-impositions and contortions listed above tend to create smooth, distorted areas but the imprint of the original set is evident and there are only few areas that look interesting - but as the set is infinite this makes for a lot! In this algorithm the fractal distortion is in the form of linear breaks and spikes creating all sorts of new and exciting areas to explore.

Bauble

What was missing up to this point was an algorithm that created nice smooth blobs that counter-balance the spikiness of the original algorithm. This distortion of the base algorithm creates just these kinds of structures - resembling beads and baubles of pure color.

Superimpose 2

There is more than one way to combine two fractals. The first attempt 'Superimpose 1' creates only a few areas of interest this version creates a lot more.

Intricate

This one, like Super1 and Super2, is a fairly simple super-imposition of fractals, in this case it creates great depths of intricate detail rather than distortions.

Daggers

Produces a wide variety of spikes that decorate the basic shapes in infinite depth.

Cubic

This started as an attempt to create a three dimensional fractal algorithm (x,y,z) but this proved uninteresting so the algorithm just uses 'z' to introduce some minor squashing and twisting.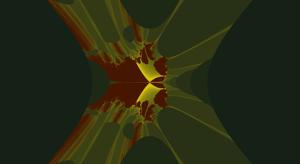

Swirls

Quite a dramatically different top level image. A variety of spikes and swirls are evident that are interesting to explore.

Face

Much of the normal fractal spiral geometry is lost in this algorithm. Instead it throws up some strange symmetric shapes that are often face like.

Flowers 1

What I had hoped to find in my hunt for a pleasing fractal algorithm was one that had many levels of undistorted, dense spirals. This family of four 'flower' fractal algorithms was purely accidental. I just tried 'random' changes to the underlying algorithm and came up with intricate and delicate images such as this.

Flowers 2

This is the second variant of the Flowers family. The main area is progressively encroached by solid color.

Flowers 3

Somewhat similar to Flowers 2 but with deeper structures and more delicate spirals.

Flowers 4

The last and most interesting of the Flowers family - asymmetric with many interesting deep areas.

Blobs

While spirals are visually pleasing the delicate structures can be overpowering, What is need are smooth areas of solid color to counterbalance the complexity and form a compositionally pleasing image. The 'blob' algorithm has areas that meet this requirement.

Slow

One of the last algorithms that were accidentally created was based on a 'mandelbulb' algorithm ➚. It uses 'sine' and 'cosine' to build up the image and that makes it extremely slow to compute. The dataset has many interesting areas that are yet to be explored.

Three dimensions

It would be very pleasing to extend these images into three dimensions. Instead of flat colors a whole 3-D surface would be possible in infinite detail to explore.

The hunt for a quick and simple 3-D algorithm is still on if you want a challenge... The original fractal is intrinsically two dimensional - it has a 'real' and 'imaginary' part which map onto 'x' and 'y'. It is tempting to think that changing the base equation from.

a = x + iy;
a2 = (x+iy) * (x+iy);


a = x + iy + jz;
a2 = (x+iy+jz) * (x+iy+jz);


Would do the trick, using the components of 'i' and 'j' as 'y' and 'z' dimensions. It creates two imaginary dimensions 'i' and 'j' (with both i² and j² = -1). However this does not give the 3-D image you might hope for - it is distorted and not that interesting. Many 3-D renderings are just spiral swirls (as if the 2D figure is just rotated around an axis) rather than 3-D landscapes.

The other main issue with 3-D is how to render it. You can choose arbitrary viewpoints and set up lights of different colors and positions - there are an infinite number of ways to view one scene. However all this takes a lot of processing time - particularly if shadows are cast. It is all much more complex than the 2-D used in our images. These effectively look directly down on a scene and use simple coloring to represent 'z' or depth.

References

Copyright © Ogless and Silurian Software 2008-2024.